Software Products

Softening-Healing Mohr-Coulomb Joint Model

The Mohr-Coulomb joint model has the following deficiencies when used to model seismicity in jointed models.

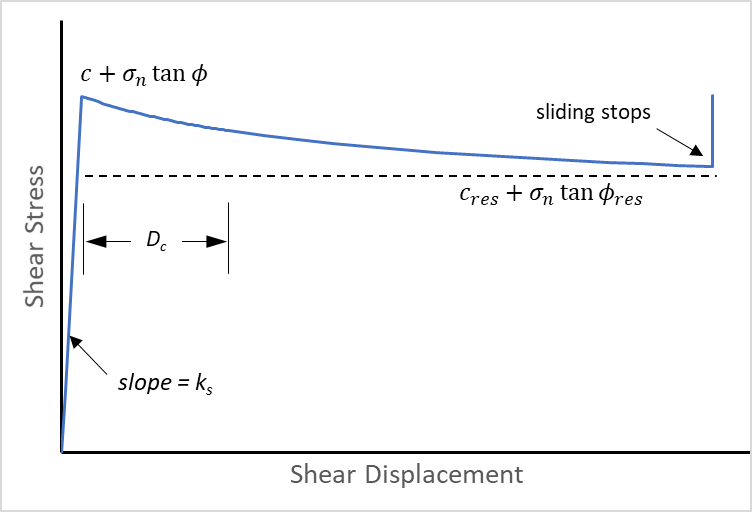
1. The stress drop is instantaneous when slipping starts — shear strength drops instantaneously from a peak to a residual value. This means that all slip events are seismic (see figure below).
2. Once slip has occurred, there is no way for the strength on the fault to recover back to the peak value. This means that stick-slip behavior is not possible.

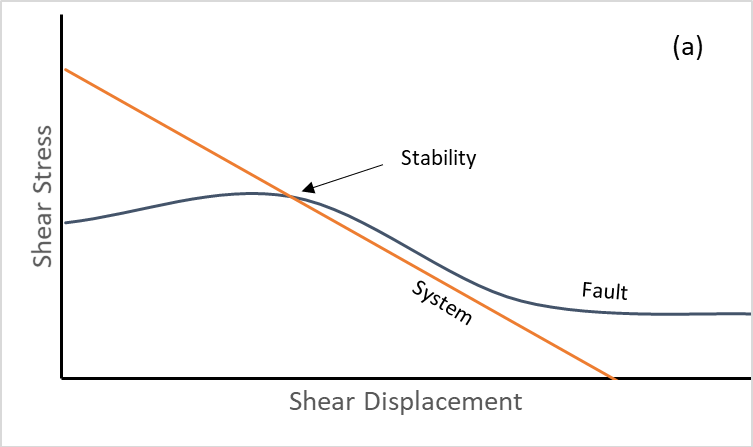
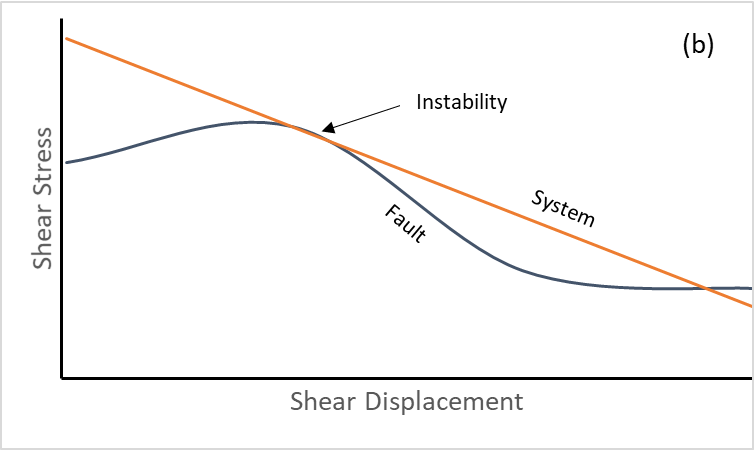
For modeling seismicity, the Softening Healing Mohr-Coulomb model is now available. It is based on the standard Mohr-Coulomb model with two additions.

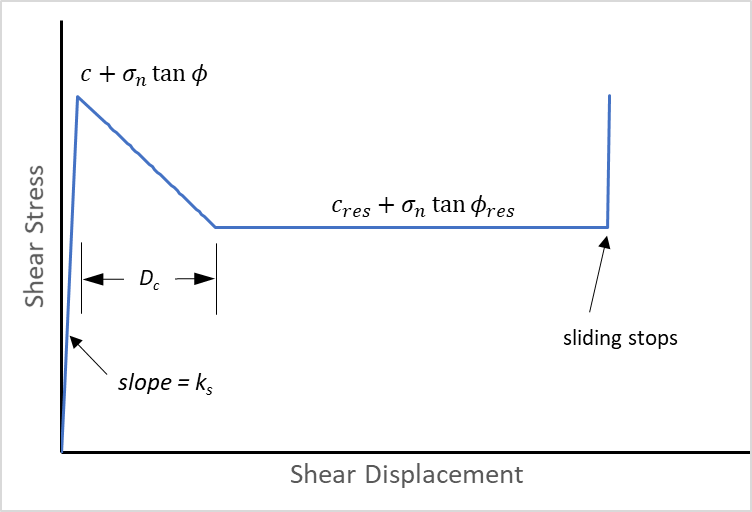
1. When the joint starts slipping, the shear strength (e.g., cohesion and friction) evolves from the peak value to the residual value over a user-specified critical slip distance D_c.
2. When slipping stops, the shear strength recovers instantaneously to the peak value.

There is no softening or healing for the tensile forces. The tensile strength drops instantaneously when the strength is exceeded (i.e., no softening) and the tensile strength remains at the residual value (i.e., no healing). Dilation (ψ) behaves in the same way as cohesion or friction.

For a non-slipping joint, the value of cohesion and friction are the peak values. When the strength is exceeded, the strength is a function of the slip distance. When the slip distance exceeds the critical slip distance, the residual values of cohesion and friction are used. Two formulations, linear and non-linear, for the evolution of shear strength are available. For the non-linear formulation, an exponent (α > 1) dictates the severity of the strength drop.

Bilinear Mohr-Coulomb Joint Model

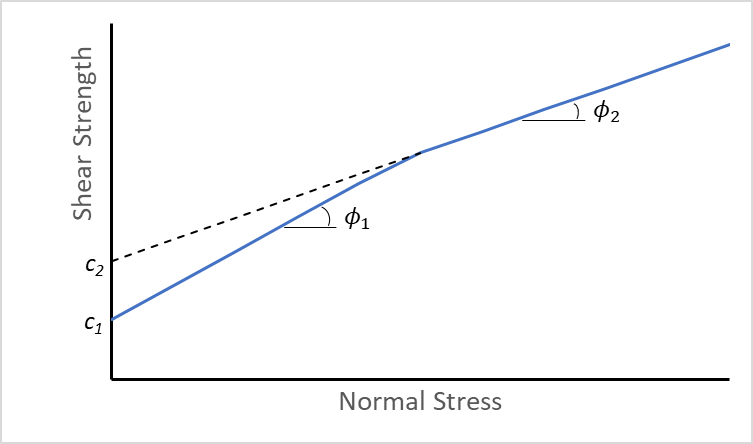
The Bilinear Mohr-Coulomb Joint Model has two different shear strength envelopes. The failure envelope changes when a critical level of normal stress is exceeded. By default, the normal stress threshold is automatically calculated at the intersection of the two failure envelopes, but the user may override this default and specify any value.

Both the peak and residual shear strengths can have bilinear envelopes and there may be different normal stress thresholds for the peak and the residual. It is also possible to specify two different values of dilation, such that dilation angle changes when the residual normal stress threshold is exceeded. If a dilation angle for the high normal stress (ψ₂) is not given, its value defaults to the dilation of the low stress region (ψ₁).

Power Law Creeping Joint Model

The creep behavior in a discontinuity is of a different nature depending on the joint surface (planar or rough) and on the filling material (gauge).

1. In unfilled discontinuities, two mechanisms can be distinguished, depending on the joint surface characteristics.
   1. In planar joints, the creep displacement is controlled mainly by an adhesion-frictional mechanism [Bowden and Curran 1984].
   2. In rough joints, the creep displacement is due to stress concentrations at asperities that cause slip as the asperities yield progressively and the shear stresses are redistributed to other intact asperities [Schwartz and Kolluru 1982, Ladanyi 1993].
2. Rock joints may naturally be filled with frictional or cohesive material, which is usually of a poor quality. In this case, the creep is controlled mainly by the characteristics of the filling material [Höwing and Kutter 1985, Malan et al. 1998].

To simulate creep due to the filling material, 3DEC uses an adaptation of Norton’s law — commonly used to model the creep behavior of soft rocks subjected to a shear load — for the joint elements.

The Power-Law-Creep joint model in 3DEC is characterized by a visco-elasto-plastic behavior in the shear direction and an elasto-plastic behavior in the normal direction. The visco-elastic and plastic elements are assumed to act in series. The visco-elastic behavior corresponds to a Norton’s law. The plastic behavior corresponds to a Mohr-Coulomb joint model.